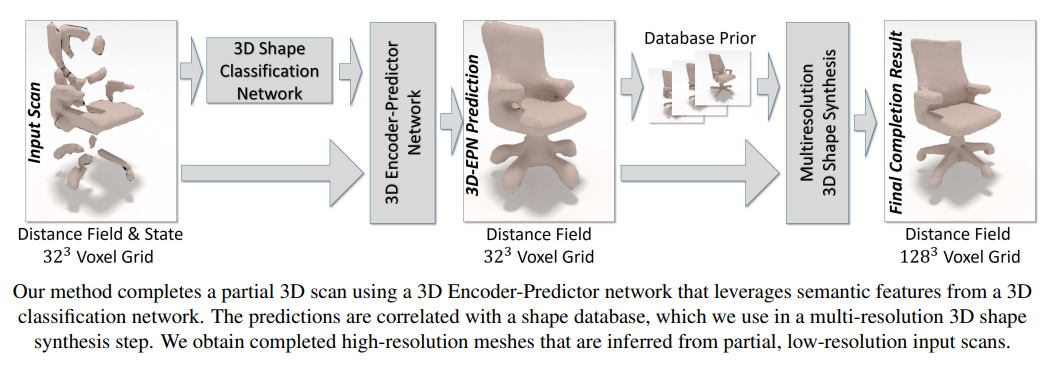
3D-EPN for shape completion

Bibtex #

@inproceedings{dai2017shape,
  title={Shape completion using 3d-encoder-predictor cnns and shape synthesis},
  author={Dai, Angela and Ruizhongtai Qi, Charles and Nie{\ss}ner, Matthias},
  booktitle={Proceedings of the IEEE conference on computer vision and pattern recognition},
  pages={5868--5877},
  year={2017}
}

Architecture #

Stage 1: Encoder - Predictor Network #

-> Give coarse estimate of structure

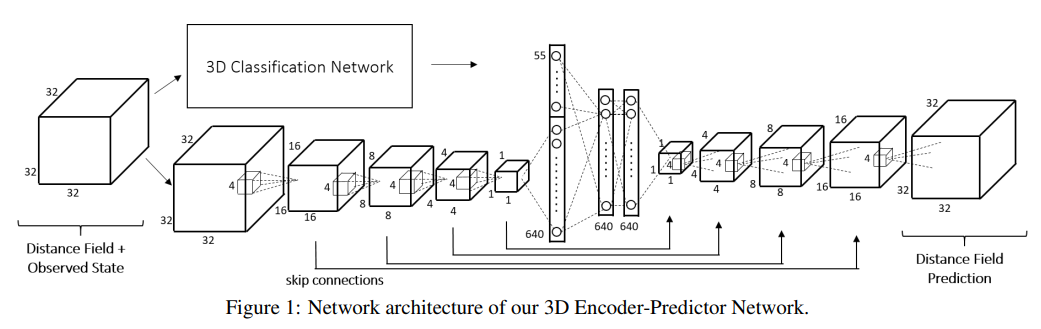
Makes use of an Distance field representation for 3d reconstruction input ()
Fairly standard set of 3D CNNs that are spatially compressing down
Using Skip Connections to keep generation closer to the input
Decoder predicting the distance field ()
3d classification network used to predict a whole shape class, so that the generator can have more information about the shape
L1 Loss Function for the distance field prediction

Insight:

When missing big parts of the shape, local methods suffer (obviously)

Parts (Omitting classification) #

Encoder: 4 layers, each one containing a 3D convolution (with kernel size 4, as seen in the visualization), a 3D batch norm (except the very first layer), and a leaky ReLU with a negative slope of 0.2. Our goal is to reduce the spatial dimension from 32x32x32 to 1x1x1 and to get the feature dimension from 2 (absolute values and sign) to num_features * 8. We do this by using a stride of 2 and padding of 1 for all convolutions except for the last one where we use a stride of 1 and no padding. The feature channels are increased from 2 to num_features in the first layer and then doubled with every subsequent layer.
Decoder: Same architecture as encoder, just mirrored: Going from num_features * 8 * 2 (the 2 will be explained later) to 1 (the DF values). The spatial dimensions go from 1x1x1 to 32x32x32. Each layer use a 3D Transpose convolution now, together with 3D batch norm and ReLU (no leaky ReLUs anymore). Note that the last layer uses neither Batch Norms nor a ReLU since we do not want to constrain the range of possible values for the prediction.
Bottleneck: This is realized with 2 fully connected layers, each one going from a vector of size 640 (which is num_features * 8) to a vector of size 640. Each such layer is followed by a ReLU activation.
Skip connections: allow the decoder to use information from the encoder and also improve gradient flow. We use it here to connect the output of encoder layer 1 to decoder layer 4, the output of encoder layer 2 to decoder layer 3, and so on. This means that the input to a decoder layer is the concatenation of the previous decoder output with the corresponding encoder output, along the feature dimension. Hence, the number of input features for each decoder layer are twice those of the encoder layers, as mentioned above.
Log scaling: You also need to scale the final outputs of the network logarithmically: out = log(abs(out) + 1). This is the same transformation you applied to the target shapes in the dataloader before and ensures that prediction and target volumes are comparable.

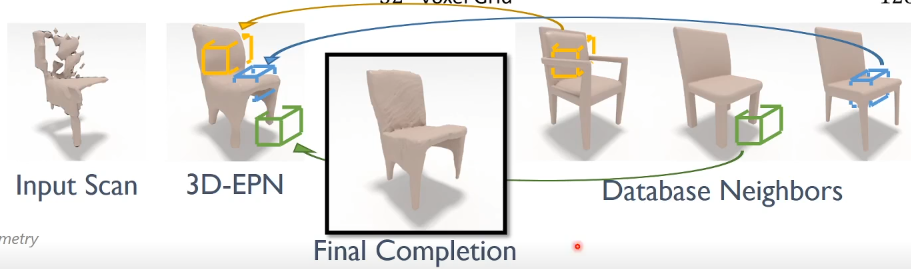
Stage 2: “Upsample” low res result #

Take coarse prediction
Database lookup and find (a couple) nearest neighbors
Then for parts of the reconstructed mesh:
- Find most similar part from the objects of (2)
- composite them in

End-To-End considerations #

This can’t easily be trained End to End since database lookups are not trivially differentiable
Training end to end would result in the first network learning to predict the most “useful” intermittant shape for retrieval and reconstruction

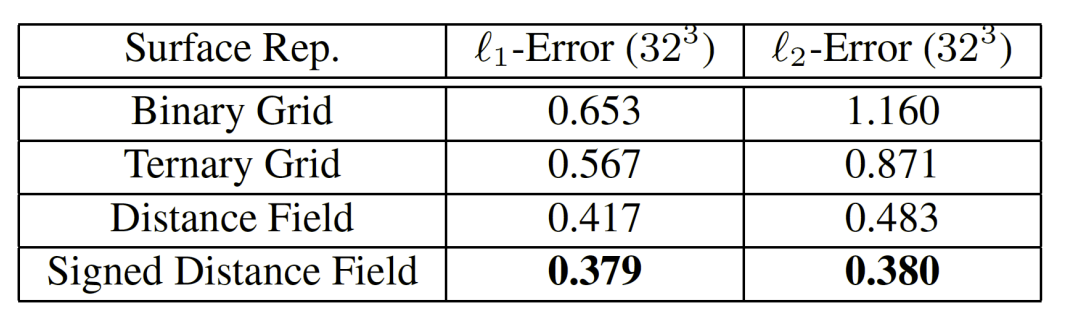
3D representation considerations #

Different 3D Representations have been tried out for the distance prediction

Implementation #

Model (Omitting classification) #

import torch
import torch.nn as nn

class ThreeDEPN(nn.Module):
    def __init__(self):
        super().__init__()

        self.num_features = 80

        self.leaky_relu = nn.LeakyReLU(0.2)
        self.relu       = nn.ReLU()

        # NOTE: 4 Encoder layers
        self.e_conv1 = nn.Conv3d(2,                   self.num_features,   kernel_size=4, stride=2, padding=1)
        self.e_conv2 = nn.Conv3d(self.num_features,   self.num_features*2, kernel_size=4, stride=2, padding=1)
        self.e_bn2   = nn.BatchNorm3d(self.num_features*2)
        self.e_conv3 = nn.Conv3d(self.num_features*2, self.num_features*4, kernel_size=4, stride=2, padding=1)
        self.e_bn3   = nn.BatchNorm3d(self.num_features*4)
        self.e_conv4 = nn.Conv3d(self.num_features*4, self.num_features*8, kernel_size=4, stride=1, padding=0)
        self.e_bn4   = nn.BatchNorm3d(self.num_features*8)

        # NOTE: 2 Bottleneck layers
        self.bottleneck = nn.Sequential(
            nn.Linear(640, 640),
            self.relu,
            nn.Linear(640, 640),
            self.relu,
        )

        # NOTE: 4 Decoder layers
        self.d_conv1 = nn.ConvTranspose3d(self.num_features*8*2, self.num_features*4, kernel_size=4, stride=1, padding=0)
        self.d_bn1   = nn.BatchNorm3d(self.num_features*4)
        self.d_conv2 = nn.ConvTranspose3d(self.num_features*4*2, self.num_features*2, kernel_size=4, stride=2, padding=1)
        self.d_bn2   = nn.BatchNorm3d(self.num_features*2)
        self.d_conv3 = nn.ConvTranspose3d(self.num_features*2*2,   self.num_features, kernel_size=4, stride=2, padding=1)
        self.d_bn3   = nn.BatchNorm3d(self.num_features)
        self.d_conv4 = nn.ConvTranspose3d(self.num_features*2,                     1, kernel_size=4, stride=2, padding=1)



    def forward(self, x):
        b = x.shape[0]
        # TODO: Pass x though encoder while keeping the intermediate outputs for the skip connections
        # Reshape and apply bottleneck layers

        # Encode
        x_e1 = self.e_conv1(x)
        x_e1 = self.leaky_relu(x_e1)

        x_e2 = self.e_conv2(x_e1)
        x_e2 = self.e_bn2(x_e2)
        x_e2 = self.leaky_relu(x_e2)

        x_e3 = self.e_conv3(x_e2)
        x_e3 = self.e_bn3(x_e3)
        x_e3 = self.leaky_relu(x_e3)

        x_e4 = self.e_conv4(x_e3)
        x_e4 = self.e_bn4(x_e4)
        x_e4 = self.leaky_relu(x_e4)

        # bottleneck
        x = x_e4.view(b, -1)
        x = self.bottleneck(x)
        x = x.view(x.shape[0], x.shape[1], 1, 1, 1)

        # NOTE: Pass x through the decoder, applying the skip connections in the process
        # Decode

        x_d1 = self.d_conv1(torch.cat((x,    x_e4), dim=1))
        x_d1 = self.d_bn1(x_d1)
        x_d1 = self.relu(x_d1)

        x_d2 = self.d_conv2(torch.cat((x_d1, x_e3), dim=1))
        x_d2 = self.d_bn2(x_d2)
        x_d2 = self.relu(x_d2)

        x_d3 = self.d_conv3(torch.cat((x_d2, x_e2), dim=1))
        x_d3 = self.d_bn3(x_d3)
        x_d3 = self.relu(x_d3)

        x_d4 = self.d_conv4(torch.cat((x_d3, x_e1), dim=1))

        x = x_d4
        x = torch.squeeze(x, dim=1)

        # NOTE: Log scaling
        x = torch.log(torch.abs(x) + 1)

        return x

Inference #

import numpy as np
import torch
from skimage.measure import marching_cubes

from exercise_3.model.threedepn import ThreeDEPN


class InferenceHandler3DEPN:
    def __init__(self, ckpt):
        """
        :param ckpt: checkpoint path to weights of the trained network
        """
        self.model = ThreeDEPN()
        self.model.load_state_dict(torch.load(ckpt, map_location='cpu'))
        self.model.eval()
        self.truncation_distance = 3

    def infer_single(self, input_sdf, target_df):
        """
        Reconstruct a full shape given a partial observation
        :param input_sdf: Input grid with partial SDF of shape 32x32x32
        :param target_df: Target grid with complete DF of shape 32x32x32
        :return: Tuple with mesh representations of input, reconstruction, and target
        """
        # NOTE Apply truncation distance: SDF values should lie within -3 and 3, DF values between 0 and 3
        input_sdf = np.clip(input_sdf, -3, 3).reshape((32,32,32))
        target_df = np.clip(target_df, 0, 3).reshape((32,32,32))

        with torch.no_grad():
            # NOTE: Pass input in the right format though the network and revert the log scaling by applying exp and subtracting 1
            input = np.expand_dims(input_sdf, axis=0)
            input = np.append(input, np.clip(input, -1, 1), axis=0)
            input[0] = np.absolute(input[0])

            input = torch.from_numpy(input).reshape((1,2,32,32,32))

            reconstructed_df = self.model(input)
            reconstructed_df = torch.exp(reconstructed_df) - 1

        input_sdf = np.abs(input_sdf)
        input_mesh = marching_cubes(input_sdf, level=1)
        reconstructed_mesh = marching_cubes(reconstructed_df.squeeze(0).numpy(), level=1)
        target_mesh = marching_cubes(target_df, level=1)
        return input_mesh, reconstructed_mesh, target_mesh