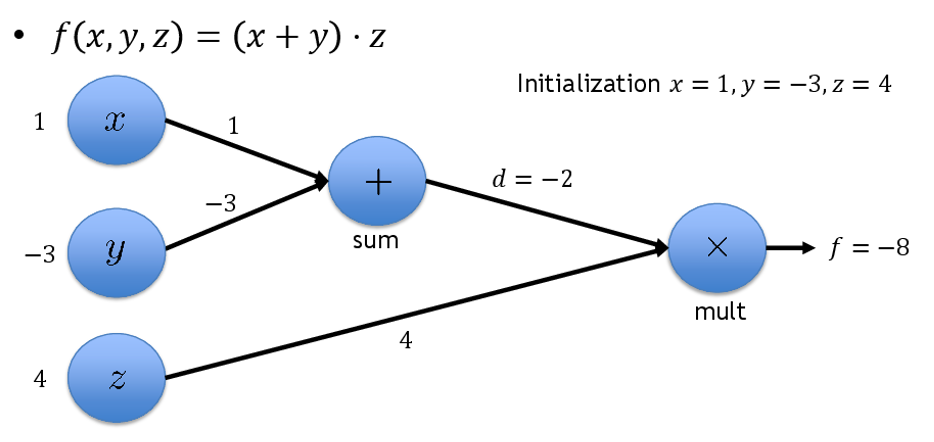
Computational Graph

• The way computation can be modelled in a Neural Network .

• Directional graph

• Matrix operations are represented as compute nodes

• Variables or scalar operators are vertex nodes

• Directional edges show the flow of inputs to vertices

• In a way the computational graph is equivalent to a syntax tree of a math expression

Evaluation #

Evaluating the neural network based on the Compute Graph and all the weights and input vector.

• Evaluate by tree walking
• starting at the leafs

Evaluation of the gradient #

For Gradient Descent we need to compute the gradient of the Loss Function (which is also part of the compute graph). So we are interested in:

1. To do this, first evaluate the loss function as described above and let each node remember it’s intermediate result.
2. Compute the partial derivatives for compute nodes. Here:
   • ; ;
   • ; ;
3. Walk the graph backwards
   • We know the parial derivative of the last node
   • We also know the evaluated values of the nodes contributing to the final node
   • So each node we can annotate with the value of their derivative under the current evaluation
   • Recursively do this until all leafs are reached
   • According to the chain rule, the resulting derivative value must be multiplied with the parents derivative value