NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

@article{mildenhall2021nerf,
  title={Nerf: Representing scenes as neural radiance fields for view synthesis},
  author={Mildenhall, Ben and Srinivasan, Pratul P and Tancik, Matthew and Barron, Jonathan T and Ramamoorthi, Ravi and Ng, Ren},
  journal={Communications of the ACM},
  volume={65},
  number={1},
  pages={99--106},
  year={2021},
  publisher={ACM New York, NY, USA}
}

Using a fully connected deep network (MLP ) to learn a function

that produces for a camera position and viewing angles a color in and visual denisty .

Similar to SIRENs

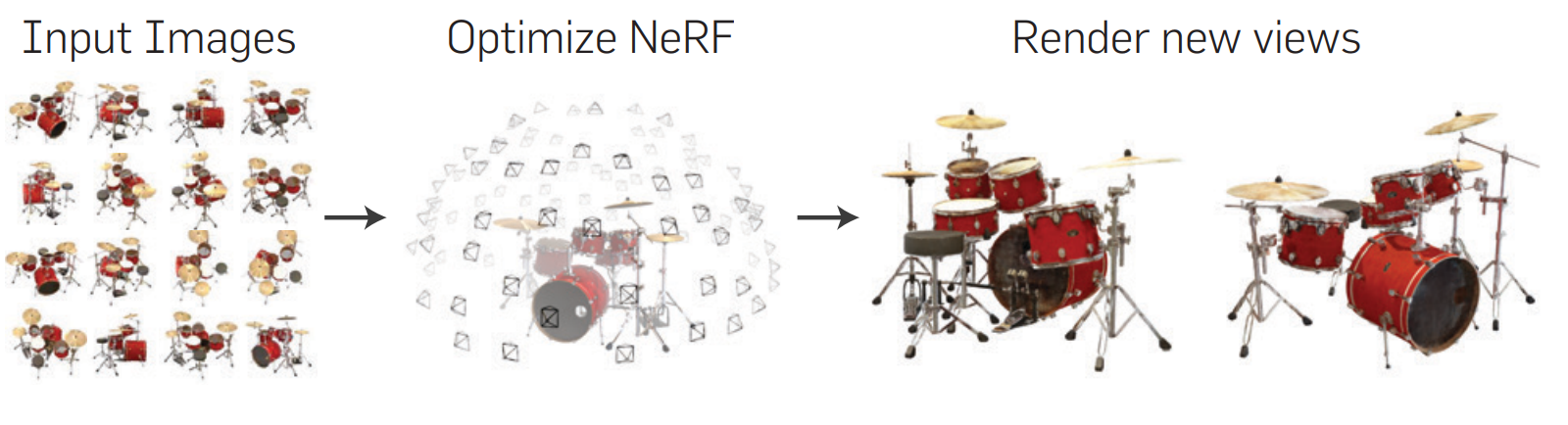
Introduction #

• The network is trained on color images with their known camera positions and directions.

• The whole network is always trained only on one scene.

• Previous approaches for novel view synthesis where never able to produce photo realistic results.

• The viewing angles are used for determining the output colors , since they could vary based on specular reflections. The visual density does not depend on the viewing angles.

• To produce an image, per pixel rays are marched through the volume and the color and densities are queried in the network. Using front to back Alpha Blending the final color for a pixel is produced.

• Since the volume rendering is itself differentiable, its result can be used as in a loss function and gradient descent can be used to train the network.

• Actually use a position encoding for the 5D input of position and viewing angles.

• Resulting scene representation (network) is much smaller than voxel representation and is furthermore not bound to a grid structure. NeRF’s scene representation is continuous.

• NeRF outperforms neural 3D representations and deep convolutional networks.

Related work #

Neural 3D shape representations #

• DeepSDF
• Occupancy Networks
• both require access to the ground truth geometry for training.

• Differentiable volumetric rendering works without 3D supervison
• previously limited to low geometric complexity and oversmoothed renderings (no positional encoding)

View synthesis and image-based rendering #

• Differentiable Rasterizer (OpenDR: An Approximate Differentiable Renderer )

• Differentiable Path Tracers (Differentiable Monte Carlo Ray Tracing through Edge Sampling )

• Both can directly optimize mesh representations.

• But mesh optimization is difficult and needs a template mesh.

• Volumetric (MPI) approaches: discrete in planes

  • Local light field fusion
  • Stereo magnification

Neural Radiance Field Scene Representation #

• In practice the viewing direction is not represented by and but rather cartesian unti vector .

• Network first predicts volumetric density based purely on position

  • 8 Fully connected layers, 256 channels per layer, using ReLU to ouput and a 256-dimensional feature vector.
  • Feature vector is concatenated with ray viewing direction to one more fully connected layer, 128 channels, ReLU to output the view depenedent RGB color.

Volume Rendering With Radiance Fields #

For a ray along direction between the near value and far value the resulting color can be calculated by integrating the colors in the volumes together with their volumetric densities along the ray.

This integral is approximated on discrete intervals, thus resulting in effective front to back Alpha Blending . The sampling intervals between and are not equidistant, to not limit the resolution of the scene’s representation. Instead the ray is divided into evenly spaced bins from each of which a sample is drawn.

Optimizing a Neural Radiance Field #

Using hierarchical sampling (1 fine and one coarse network). Use the coarse network to find geometry and sample near geometry in the fine network. Calculate loss over both networks independenty and optimize independenty.

Positional encoding #

• Needed for high-resolution complex scenes

• deep networks are biased toward learning lower frequency functions

  • To combat, transfrom the input into a higher dimensional space using high frequency functions, and train the network on the modified input (of course also use transformed input for inference later, too)
  
  • is then applied to all 3 components of the viewing position and all 3 components of the viewing direction .
  • is normalized such that each component is

• The paper uses for the position and for the viewing direction

  • Resulting in a input layer of size

Implementation details #

Loss function is just the total squared error over the resulting RBG color for rays in the batch .

The paper used batch size of 4096 rays each sampled at positions and the ADAM optimizer.