3d Shape Alignment
Input #
- 2 shapes
and
with partial overlap
General problem #
-
find a rigid transform (preserves distances of two points before and after transform) to minimize the distance between
and
- for distance measure
- and rigid transform
- for distance measure
Distance Problem #
- What is the distance between two shapes?
- If we have corresponding points, we can get the distance between them
- But generally we don’t have them
Overlap Problem #
The distance metric should give a good match if the overlapping parts of the shaps are matching.
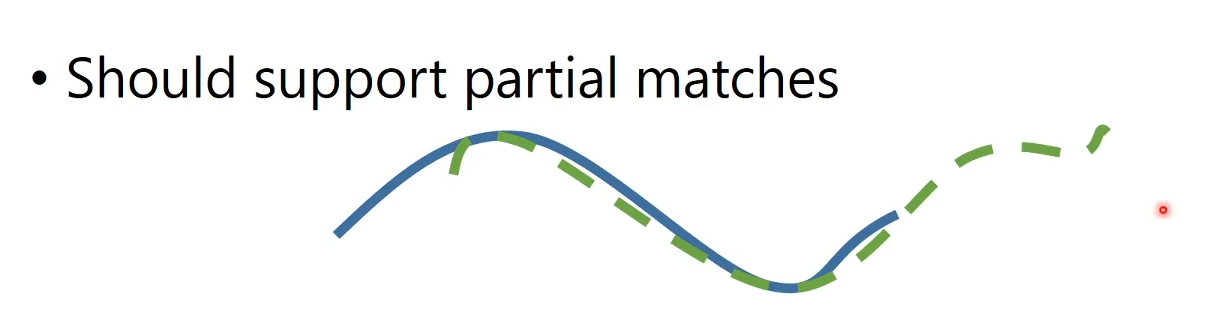
If you took the original measurements, then maybe you even know how much the shapes should roughly overlap.
High level solution #
- Given shaped
and
- Establish correspondences between
and
- Find optimal transform that best aligns correspondences based on a
distance metric (like the
norm )
- Generally, the more restriced the problem is, the easier it is to find a solution
Transform estimate #
- 6 degrees of freedom: translation and rotation (because rigid transform)
- estimate with more correspondences
overdetermined problem
- More DOF for more generell movements
Solution when knowing corresponding points #
For all points in Shape
and the corresponding points
of
shape
.
Considering a coordinate system centered at the mean of the .
We can split up the solving fot translation and rotation by first fixing
the tanslation. According to the `translation` part in the problem,
if we align both shapes by their centroids, we only have to find the
corresponding rotation: Remove translation by mean centering.
Now both shapes should be centered at the origin.
Solve this by computing the SVD (singular value decomposition) of
Define:
Then: The optimal rotation will be:
The translation has to be recomputed then by taking the mean of the rotated .
<img src="/ltximg/3d_shape_alignment_cc8e04174153a3c8a4d521aefddb008d9de51aa3.svg" alt="3d_shape_alignment_cc8e04174153a3c8a4d521aefddb008d9de51aa3.svg" class="org-svg" />
then