Iterative Closest Points

Method that can be used for alinging shapes iteratively. it works like this:

1. estimate some correspondences
2. solve transformation using them
3. repeat

How to find correspondences? #

• Assume that closest points correspond
• This will converge iteratively if starting postitions are “close enough”

Runtime analysis #

• Each iteration
  1. Finding closest points:
     • per point naively
     • Therefore in total
  2. Compute optimal alignment
  3. Update scene

• Finding closest correspondences can be sped up using acceleration structures like KD-Trees to
• Finding the closest points for all points is then in

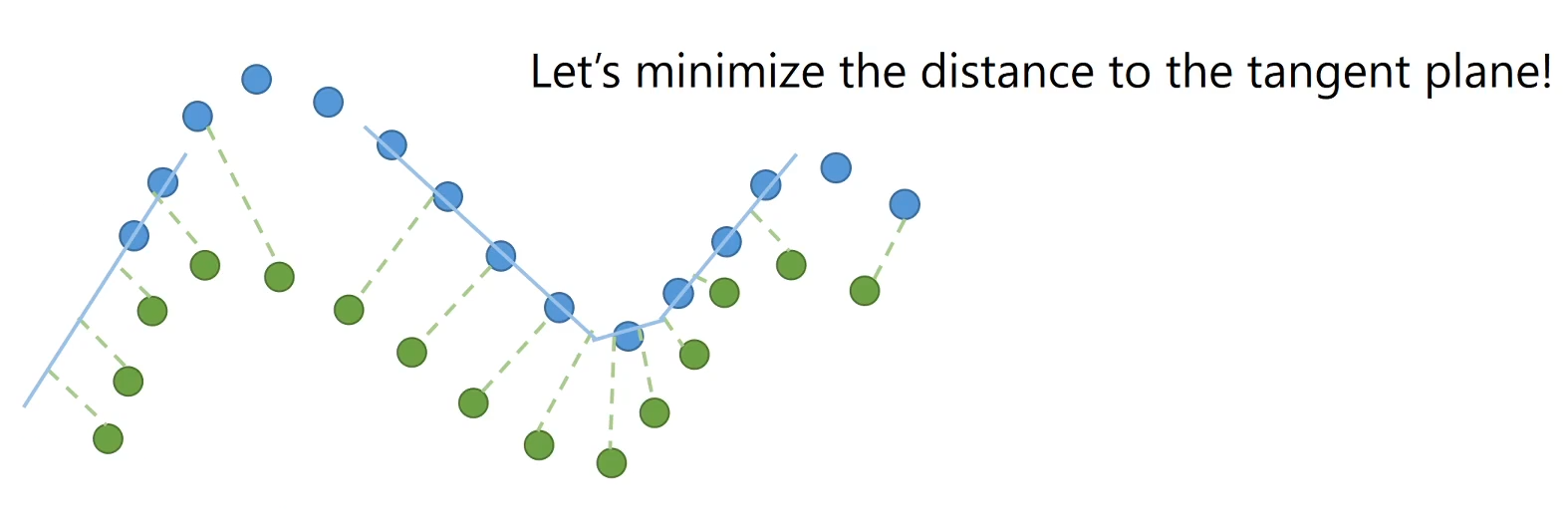
Variations / Improvements #

• Instead of trying to minimize the distance between the closest points, we can try to instead minimize the distance of points of to the tangent planes of nearest points in .
• Drawback: No closed form solution
• Benefit: Converges faster than taking just aligning point-to-point