Linear vs sRGB

Traditional formulation #

linear_vs_srgb_8f5a68cbb7672aecbd329047d7d29c9cf880c503.svg

for

linear_vs_srgb_5b49c1984ca77d2a085cc4877ad66400c42f689f.svg

in sRGB.

linear_vs_srgb_2f80562e643bda9defb49754644a0516110e9de0.svg

for

linear_vs_srgb_17c7202289182790f04830597e1dbec0b9c1d6f8.svg

in linear.

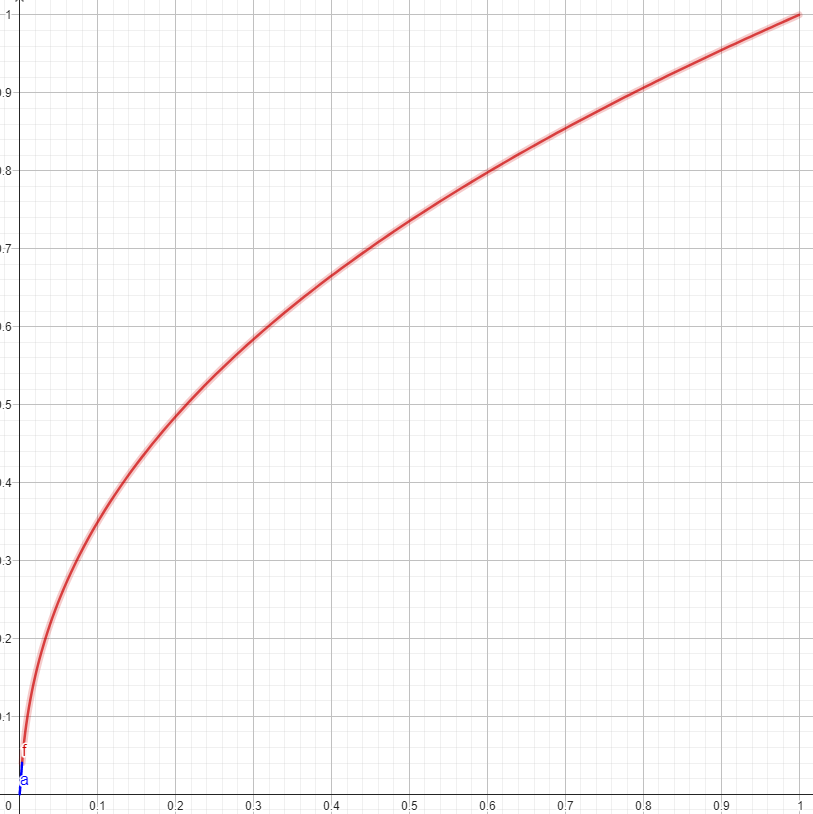
Figure 3: Traditional linear to sRGB implementation.

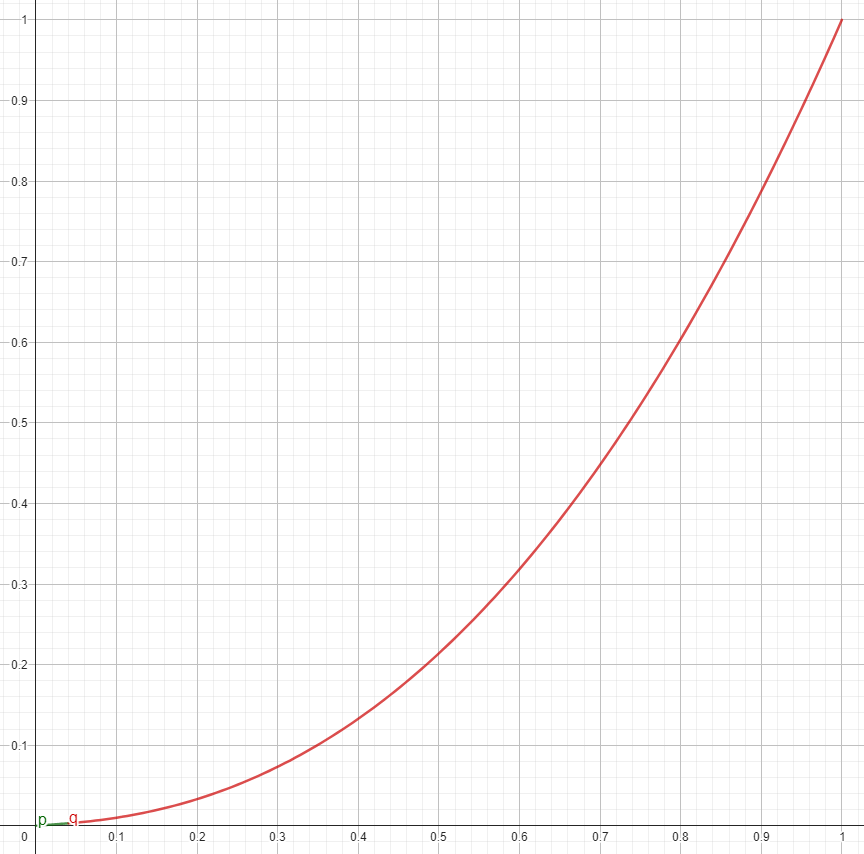
Figure 4: Traditional sRGB to linear implementation.

which together translates to

float sRGB_to_linear(float s) {
    if (s <= 0.04045)
        return s / 12.92;
    return powf((s+0.055)/1.055, 2.4);
}

float linear_to_sRGB(float l) {
    if (l <= 0.0031308)
        return l * 12.92;
    return 1.055 * powf(l, 1/2.4) - 0.055;
}

V3 linear_to_sRGB(V3 linear) {
    V3 result = {
        linear_to_sRGB(linear.r),
        linear_to_sRGB(linear.g),
        linear_to_sRGB(linear.b),
    };
    return result;
}
V3 sRGB_to_linear(V3 srgb) {
    V3 result = {
        sRGB_to_linear(srgb.r),
        sRGB_to_linear(srgb.g),
        sRGB_to_linear(srgb.b),
    }

    return result;
}

More precise cutoff points #

claims the cut-off point of 0.0404482362771082 for sRGB_to_linear and 0.00313066844250063 for linear_to_sRGB are more precise than the usual 0.0

Alternative formulations #

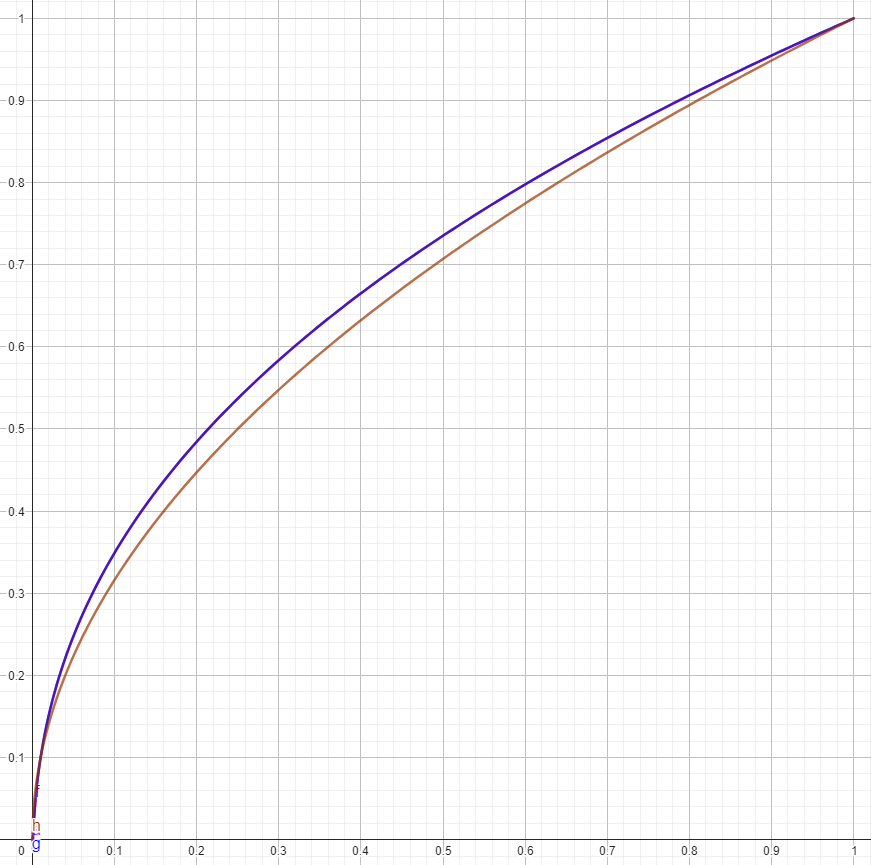
Figure 5: Alternative linear to sRGB (the traditional formulation also shown behind blue). Blue: version from jai-modules. Brown: even cheaper Handmade Hero version.

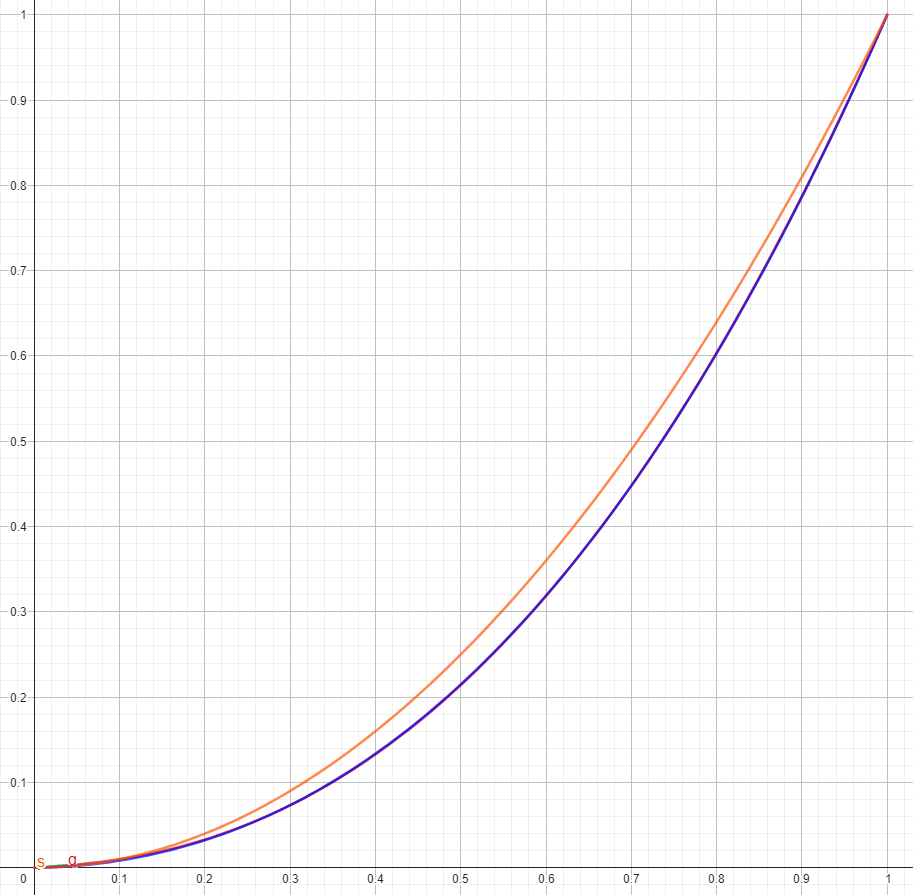
Figure 6: Alternative sRGB to linear implementation (the traditional formulation also shown behind blue). Blue: version from jai-modules. Brown: even cheaper Handmade Hero version.

Implementation from jai modules #

float linear_to_srgb_fast(float x) {
    float s1 = sqrtf(x);
    float s2 = sqrtf(s1);
    float s3 = sqrtf(s2);
    return 0.66200269 * s1 + 0.6841221 * s2 - 0.3235836 * s3 - 0.022541147 * x;
}

float srgb_to_linear_fast(float x) {
    return x * (x * (x * 0.30530601 + 0.68217111) + 0.012522878);
}

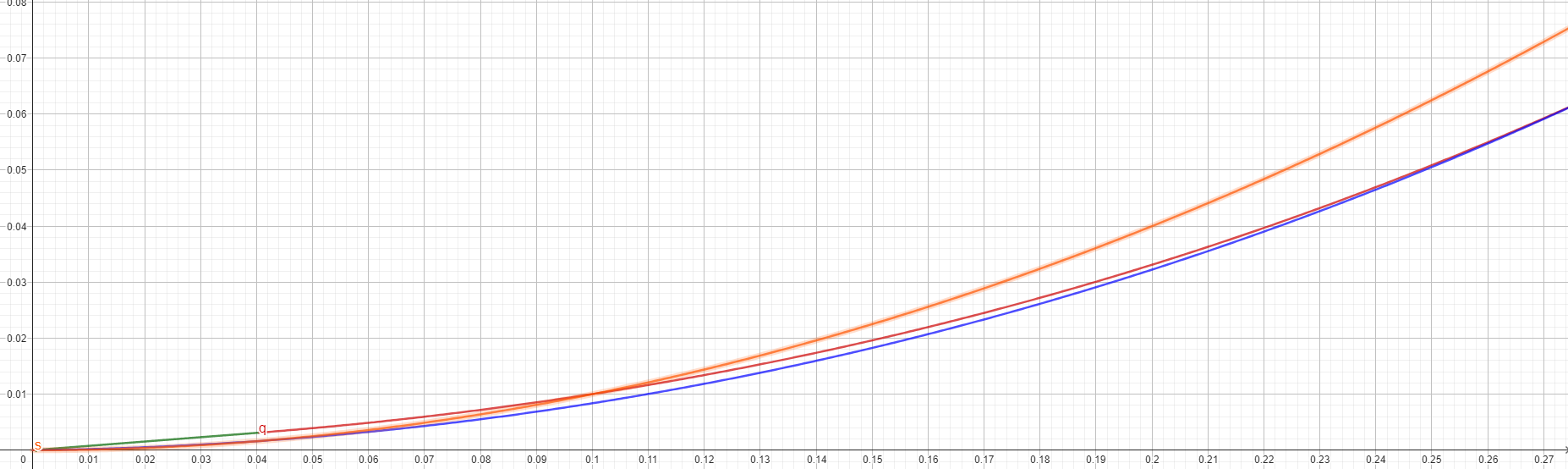
Figure 7: The jai version looks really close, it only differs in the really low-x range. Brown version is the worse Handmade Hero approximation.

This implementation resembles the formulation of , with slightly different constants.

Implementation from Handmade Hero #

float linear_to_srgb_super_fast(float x) {
    return sqrtf(x);
}

float srgb_to_linear_super_fast(float x) {
    return x * x;
}

References #

: https://matt77hias.github.io/blog/2018/07/01/linear-gamma-and-sRGB-color-spaces.html : https://entropymine.com/imageworsener/srgbformula/ : https://twitter.com/schneckerstein/status/1638200902027821058 : https://chilliant.blogspot.com/2012/08/srgb-approximations-for-hlsl.html