Mollweide Pojection

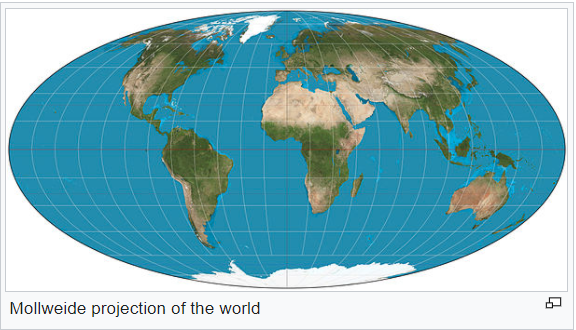
The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.

The projection has the aspect ratio of 2:1.

Lat+Lng to Mollweide coordinates #

Given latitude and longitude as well as the meridian longitude (which will be in the center of the projection), the auxilary angle is defined as:

Using it we can define the uv coordinates and , where is the radius of the globe to be projected. The formular is set up such that the resulting area is the same as the surface of the projecting globe.

If we only only care about uv coordinates and , the formular gets simpler.

Finding numerically #

can be found by iterating the following equations.

Mollweide coordinates to Lat+Lng #

For given uv coordinates and one can find the latitude and longitude as follows:

In Code #

void lat_lng_to_mollweide(f32 phi, f32 lambda, f32* out_x, f32* out_y) {
    f32 theta = phi;
    f32 old_t;
    do {
        old_t = theta;
        f32 denom = cosf(theta);

        theta = theta - (2*theta + sin(2*theta) - pi*sin(phi)) /
                        (4 * denom * denom);

    } while(fabs(old_t - theta) > 0.001f);

    *out_x = lambda * cosf(theta) / pi; // [-1;     1]
    *out_y = sinf(theta) / 2;           // [-0.5; 0.5]
}

void mollweide_to_lat_lng(f32 x, f32 y, f32* out_phi, f32* out_lambda) {
    f32 sqrt_2   = sqrtf(2.0f);
    f32 theta    = asinf(y/sqrt_2);
    *out_phi     = asinf((2.0f*theta + sin(2.0f*theta))/pi);
    *out_lambda  = (x*pi)/(2.0f*sqrt_2*cos(theta));
}